PageRank网页排序算法

1，定义

将整个互联网视为一个巨大的有向图$G=(V,E)$$G = (V , E)$，网页构成有向图的节点，网页间的超链接构成有向图的边，据此构建一个随机游走模型，即一阶马尔可夫链¹。

在这个模型中，为每个网页设定一个初始化的PageRank值，表示用户停留在该网页的概率，网页浏览者会随机地、按照等概率地跟随一个页面上的任何一个超链接到另一个页面，并持续这种随机跳转。

在长时间内，这种随机跳转的行为会形成一个稳定的模式（马尔可夫链的平稳分布），每个网页的 PageRank 值，即用户停留在每个网页的概率收敛到一个稳定值。

直观上，如果指向网页$i$$i$的超链接越多、能跳转到网页$i$$i$的上游网页$j$$j$的PageRank越高，随机跳转到网页$i$$i$的概率也就越高，网页$i$$i$的PageRank值就越高，网页也就越重要²。

2，数学表示

有向图的状态转移矩阵定义为$\mathbf{M}=[m_{i,j}{]}_{n\times n}$$\mathbf M=[m_{i,j}]_{n\times n}$，其中$m_{i,j}$$m_{i,j}$表示$\mathbf{M}$$\mathbf M$的第$i$$i$行第$j$$j$列，也即节点$j$$j$转移到节点$i$$i$的概率，$\mathbf{M}$$\mathbf M$具有如下性质：

• 如果$j,i$$j,i$间存在边，从节点$j$$j$出发到达节点$i$$i$的概率等于节点$j$$j$出度的倒数，否则转移概率为0。定义$\mathbb{v}(j)$$\mathbb v(j)$为节点$j$$j$指向页面的集合，$L(\mathbb{v}(j))$$L(\mathbb v(j))$为节点$j$$j$的出度

  $$m_{i,j}=\{\begin{array}{ll}\frac{1}{L(\mathbb{v}(j))}& \text{if }j,i\text{间}\text{存}\text{在}\text{指}\text{向}\text{关}\text{系},\\ 0& \text{if }j,i\text{间}\text{不}\text{存}\text{在}\text{指}\text{向}\text{关}\text{系}.\end{array}$$

• 如果节点$j$$j$出度不为0，从节点$j$$j$出发到达其他节点的概率和为1：$\sum _i{m}_{i,j}=1$$\sum_im_{i,j}=1$

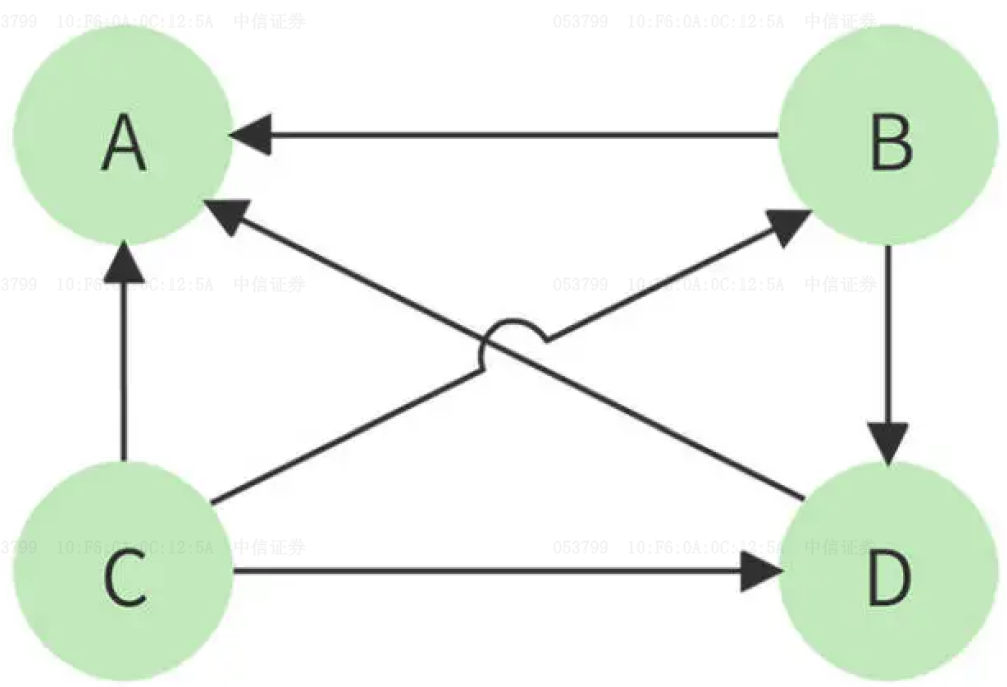
图示³节点转移关系的状态转移矩阵可以表示为

定义$t$$t$时刻所有节点的PageRank值为向量${\mathbf{R}}_t=[r_t^i{]}_n$$\mathbf {R}_t=[r_t^i]_n$，其中$r_t^i$$r_t^i$表示$t$$t$时刻停留在节点$i$$i$的概率，满足$\sum _i{r}_t^i=1$$\sum_ir_t^i=1$，0时刻的状态分布向量初始化为${\mathbf{M}}_0=[\frac{1}{n}{]}_n$$\mathbf M_0=[\frac{1}{n}]_{n}$，则$t+k$$t+k$时刻的状态分布向量

当经过足够长时间，上述随机游走过程达到马尔可夫链的平稳分布，${\mathbf{R}}_t$$\mathbf R_t$收敛至$\mathbf{R}$$\mathbf R$

此时由于状态已经收敛，满足

要保证上述马尔可夫过程具有稳态分布，需要满足以下条件

• 不可约性: 有向图是连通图，没有孤立的节点。

• 非周期性: 对于任何状态，返回到该状态的步数不是一个固定的周期。

• 正常返还性: 每个状态都会被反复访问，且访问的平均间隔时间是有限的。

由节点间链接指向关系构成的随机游走过程不一定同时满足上述三个条件，即不保证存在平稳状态。对此引入常数矩阵$\mathbf{E}/n$$\mathbf E/n$，其中$\mathbf{E}$$\mathbf E$为$n\times n$$n\times n$全1矩阵，状态转移过程更新为

其中$d(0\le d\le 1)$$d(0\leq d\leq1)$为阻尼因子，表示为节点以$d$$d$的概率按照链接跳转，以$(1-d)$$(1-d)$的概率任意跳转。

• $\mathbf{E}/n$$\mathbf E/n$的存在使得浏览者以$\frac{1}{n}$$\frac{1}{n}$的概率跳转到任意页面，而不仅仅是通过超链接，有向图是连通图，因此随机游走过程是不可约的。

• 每个状态都有正概率转移到自身（$d\mathbf{M}+\frac{(1-d)\mathbf{E}}{n}$$d\mathbf M+\frac{(1-d)\mathbf E}{n}$对角线元素为正），说明每个状态的周期是1，因此上述过程是非周期的。

• 由于上述过程是不可约和非周期的，且所有状态都有正概率转移到自身，这意味着从任何状态出发，平均返回到该状态的时间是有限的，因此上述过程是正常返还的。

3，数值求解

迭代求解

利用迭代公式${\mathbf{R}}_{t+k}=(d\mathbf{M}+\frac{(1-d)\mathbf{E}}{n}{)}^k{\mathbf{R}}_t$$\mathbf R_{t+k}=(d\mathbf M+\frac{(1-d)\mathbf E}{n})^k\mathbf R_t$迭代求解，直至${\mathbf{R}}_t$$\mathbf R_t$趋于稳定，求解代码如下

1
def pagerank_iter(M, d, tol=1.0e-6):
2
    n = M.shape[0]
3
    pagerank_vector = np.ones(n) / n
4
    base = (1 - d) / n * np.ones(n)
5
    while (True):
6
        new_rank = d * M @ pagerank_vector + base
7
        if np.linalg.norm(new_rank - pagerank_vector, ord=1) < tol:
8
            return new_rank
9
        pagerank_vector = new_rank

代数求解

当经过足够长时间，达到马尔可夫链的平稳分布，${\mathbf{R}}_t$$\mathbf R_t$收敛至$\mathbf{R}$$\mathbf R$时，满足

其中$\mathbf{ER}=[\sum _j{\mathbf{R}}_j{]}_n=[1{]}_n=\mathbf{1}$$\mathbf {ER}=[\sum_j\mathbf R_j]_{n}=[1]_{n}=\mathbf 1$为全1列向量，$\mathbf{I}$$\mathbf I$为$n\times n$$n\times n$单位矩。上述方法求解代码如下

​x
1
def pagerank_algebraic(M, d):
2
    I = np.eye(n)
3
    coeff_matrix = I - d * M
4
    b = np.ones(n) * (1 - d) / n
5
    pagerank_vector = scipy.linalg.solve(coeff_matrix, b)
6

7
    return pagerank_vector
8

MapReduce方式求解

根据迭代公式

可知对于$t+1$$t+1$时刻的节点$i$$i$，其PageRank值为

其中$\mathbb{m}(i)$$\mathbb m(i)$为存在指向节点$i$$i$的节点的集合，$\mathbb{v}(i)$$\mathbb v(i)$为节点$i$$i$指向节点的集合。

在$t$$t$时刻，节点$i$$i$需要汇集在$t-1$$t-1$时刻所有指向$i$$i$的节点$j\in \mathbb{m}(i)$$j \in \mathbb m(i)$的PageRank值，用于更新$i$$i$在$t$$t$时刻的PageRank值，同时也需要向所有$i$$i$ 节点指向的节点$k\in \mathbb{v}(i)$$k \in \mathbb v(i)$分发$i$$i$的PageRank值，用于$t+1$$t+1$时刻节点$k$$k$更新PageRank值。

整个计算过程可以拆分为Map与Reduce两个过程，利用分布式计算框架迭代更新，由于互联网网页数量是万亿级的数字，由于上述的迭代解法和代数解法需要在单机上运行，将无法处理万亿级数据，MapReduce方法则可以解决单机计算的性能瓶颈问题。

Map过程接收节点$j$$j$的编号、PageRank值和节点$j$$j$指向节点集合$v(j)$$v(j)$为输入，向可跳转节点$i$$i$传递当前在$j$$j$节点时，下一时刻游走到$i$$i$节点的条件概率$P(i|j)$$P(i|j)$，用于更新$t+1$$t+1$时刻$i$$i$的PageRank值，完成节点$j$$j$向可跳转节点的随机游走过程。同时向节点$j$$j$本身传递$t$$t$时刻的PageRank值和$v(j)$$v(j)$，用于判断$j$$j$在$t+1$$t+1$时刻更新后PageRank值是否收敛。

Reduce过程按照节点编号$i$$i$汇集所有指向他的节点$j\in \mathbb{m}(i)$$j \in \mathbb m(i)$的条件概率$P(i|j)$$P(i|j)$，更新$t+1$$t+1$时刻的PageRank值，并判断是否收敛，同时向下传递节点$i$$i$编号，$\mathbb{v}(i)$$\mathbb v(i)$和PageRank，用于下一轮MapReduce过程。

整个过程的伪代码如下

xxxxxxxxxx
24
1
Map(nid, node):
2
    yield nid, ('node', node)
3
    
4
    outlinks ,rank = unpack(node)
5
    for (outlink in outlinks):
6
        yield outlink, ('pagerank', rank / len(outlinks))
7

8
Reduce(nid, values):
9
    outlinks = []
10
    totalRank = 0
11
    oldRank = 0
12

13
    for (val in values):
14
        label, content = unpack(val)
15
        if label == 'node':
16
            outlinks = content[0]
17
            oldRank = content[1]
18
        else
19
            totalRank += content
20
    
21
    totalRank = (1 - d)/n + (d * totalRank)
22
    if check_err(oldRank, totalRank)> Thread:
23
        unconverted+=1
24
    yield nid, ('node', (outlinks,totalRank))

以下使用mrjob包完成MapReduce计算任务实现，完整代码可见PageRank。

xxxxxxxxxx
55
1
import os
2
import shutil
3
import time
4

5
import numpy as np
6
from mrjob.job import MRJob
7
from mrjob.protocol import JSONProtocol
8

9
from tools import check_err, load_data
10

11

12
class PageRank(MRJob):
13
    INPUT_PROTOCOL = JSONProtocol
14

15
    def configure_args(self):
16
        super(PageRank, self).configure_args()
17
        self.add_passthru_arg('--n', type=int)
18
        self.add_passthru_arg('--d', type=float)
19

20
    def mapper(self, nid, node):
21
        # 流向下一层更新pagerank处理
22
        yield nid, ('node', node)
23

24
        # 指向的其他节点, 当前节点pagerank
25
        adjacency_list, pagerank = node
26
        if len(adjacency_list) != 0:
27
            p = pagerank / len(adjacency_list)
28
            # 当前节点对他指向节点的贡献
29
            for adj in adjacency_list:
30
                yield adj, ('pagerank', p)
31

32
    def reducer(self, nid, values):
33
        # Initialize sum and node
34
        cur_sum = 0
35
        node = [[[], 0]]
36

37
        for val in values:
38
            label, content = val
39
            # 数据类型是node, 保存外链和pagerank值
40
            if label == 'node':
41
                node[0][0] = content[0]
42
                node[0][1] = content[1]
43
            # 数据类型是pagerank，计算所有指向当前节点vi的节点vj对vi的共享
44
            elif label == 'pagerank':
45
                cur_sum += content
46

47
        # 更新节点的PageRank值
48
        cur_sum = cur_sum * self.options.d + (1 - self.options.d) / self.options.n
49
        # 如果PageRank变化大于阈值，则视为未收敛
50
        if abs(cur_sum - node[0][1]) > 1e-9:
51
            self.increment_counter('nodes', 'unconverted_node_count', 1)
52

53
        node[0][1] = cur_sum
54
        node = tuple(*node)
55
        yield nid, node

4，验证

考虑一个n=8个节点构成有向图，转移矩阵初始化为

阻滞因子$d=0.85$$d=0.85$，状态分布向量初始化${\mathbf{R}}_0=[1/8{]}_8$$\mathbf R_0=[1/8]_8$。

• 迭代法耗时1.009毫秒收敛，收敛值为

  [0.14564, 0.18355, 0.04577, 0.29856, 0.02672, 0.01875, 0.02632, 0.03820] 迭代误差为7.480E-7。

• 代数求解耗时5.991 毫秒，收敛值为 [0.14564, 0.18355, 0.04577, 0.29856, 0.02672, 0.01875, 0.02632, 0.03820] 迭代误差为6.9388E-17

• MapReduce方式求解耗时57.1386秒，收敛值为 [0.14563, 0.18354, 0.04577, 0.29855, 0.02671, 0.01875, 0.02632, 0.03820] 迭代误差为1.4726e-07

迭代法和代数求解可以快速得到结果，并且代数求解可以获得最佳结果，但相较于其他方法，矩阵求逆时间复杂度较高，并且迭代法和代数求解只能在单机上运行，可运算数据规模受限。

MapReduce法求解时，由于每轮Map过程和 Reduce过程都涉及1次文件读写以及对象序列化和反序列化，且无法实现矩阵并行化计算，计算耗时最长，但是可以利用多机并行计算不受单机节点性能限制。

5，思考

通过上一小结发现MapReduce方式由于无法实现矩阵并行化计算，是性能较差的主要原因之一。观察公式

可以发现，迭代过程的矩阵运算可以分块进行。将上述表达式简化为$\mathbf{Y}=\mathbf{MR}+\mathbf{B}$$\mathbf Y=\mathbf{MR}+\mathbf B$，考虑将$\mathbf{M}$$\mathbf M$划分为$p\times q$$p\times q$个子阵，横向分割线下标为$[i_1,i_2,...,i_p]$$[i_1,i_2,...,i_p]$，纵向分割线下标为$[j_1,j_2,...,j_q]$$[j_1,j_2,...,j_q]$，同样将$\mathbf{R}$$\mathbf R$和$\mathbf{B}$$\mathbf B$划分为$q$$q$个子阵，横向分割线下标为$[j_1,j_2,...,j_q]$$[j_1,j_2,...,j_q]$，$\mathbf{Y}$$\mathbf Y$划分为$p$$p$个子阵列，横向分割线下标为$[i_1,i_2,...,i_p]$$[i_1,i_2,...,i_p]$。$\mathbf{Y}$$\mathbf Y$的第$i$$i$个子阵可以表示为

通过计算任务的拆分，将子阵分发到不同计算节点上，可以将大尺度矩阵运算切分为多个MapReduce小尺度矩阵运算子任务，将循环迭代计算替换为矩阵并行计算，缩短运算时间。以下为分块运算正确性验证，具体MapReduce任务待实现。

xxxxxxxxxx
32
1
import random
2

3
import numpy as np
4

5
np.random.seed(114514)
6

7
# 分块计算Y=M@PR+B
8
n = 128
9
ki, kj = 7, 11  # ki,kj为分割的块数
10
M = np.random.randn(n * n).reshape(n, n)
11
PR = np.random.randn(n, 1).reshape(n, 1)
12
B = np.ones((n, 1)) * (1 - 0.85) / n
13

14
# 生成横向和纵向的分割点
15
block_i = sorted([0] + random.sample(range(1, n), ki - 1) + [n])
16
block_j = sorted([0] + random.sample(range(1, n), kj - 1) + [n])
17

18
Y = np.zeros_like(B) 
19

20
# 分块处理
21
for i in range(ki):
22
    start_i = block_i[i]
23
    end_i = block_i[i + 1]
24
    for j in range(kj):
25
        start_j = block_j[j]
26
        end_j = block_j[j + 1]
27
        Y[start_i:end_i] += M[start_i:end_i, start_j:end_j] @ PR[start_j:end_j]
28
Y += B  
29

30
# 3.51043408855362e-14
31
print(np.linalg.norm(Y - (M @ PR + B)))
32

6，代码结构

完整代码可见PageRank：

• tools.py中的generate_sparse_matrix函数用于生成随机状态转移矩阵，方法将$\mathbf{M}$$\mathbf M$写入data/input.txt中，数据格式为"节点编号 [指向节点集合, 初始PageRank值]"。check_err函数用于计算当前$\mathbf{R}$$\mathbf R$在前后两次迭代间的差值。

• matrix_pagerank.py定义了问题的迭代法pagerank_iter和代数解法pagerank_algebraic。

• mapredue_pagerank.py定义了问题的MapReduce解法。

• martix_mr_pagerank.py验证了迭代方法中矩阵分块计算的正确性。

• data文件夹包含输入数据input.txt，以及MapReduce方法的输出结果。

7，引用